プログラムや計算で四捨五入をすることは多いと思います。ところで勘定系のプログラムを扱った人は銀行丸めというのを聞いたことがあるかも知れません。
なぜ普通の四捨五入とは別にそんなものがあるのかを解説します。
四捨五入は誤差が蓄積される
1.0から1.9までの9つの数値を整数にする例で考えてみます。1.0か2.0のどちらかになります。
切り捨てになるのは1.1, 1.2, 1.3, 1.4の4通り。
切り上げになるのは1.5, 1.6, 1.7, 1.8, 1.9の5通り。
そのうち、下図のように1.5の場合だけ切り上げと切り捨てが相殺されません。
そのため、ランダムに1.0から1.9の数値が現れたとき、+0.5の誤差が積み上がりそうなことがイメージできます。
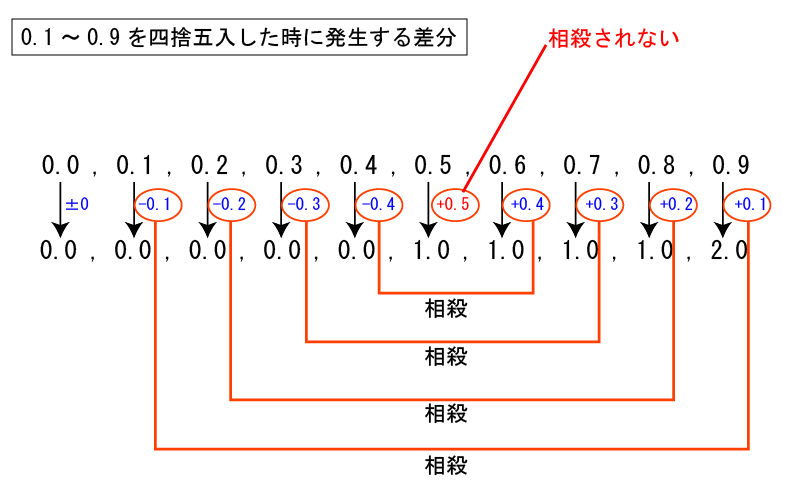
切り捨てられる値は -0.1, -0.2, -0.3, -0.4で 平均-0.25。
切り上げになる値は +0.5, +0.4, +0.3, +0.2, +0.1で 平均+0.3です。
大量のデータを扱うと平均的にこの差が蓄積し、実際の合計値との誤差が大きくなっていきます。
銀行丸めだと誤差が小さい
銀行丸めのイメージ
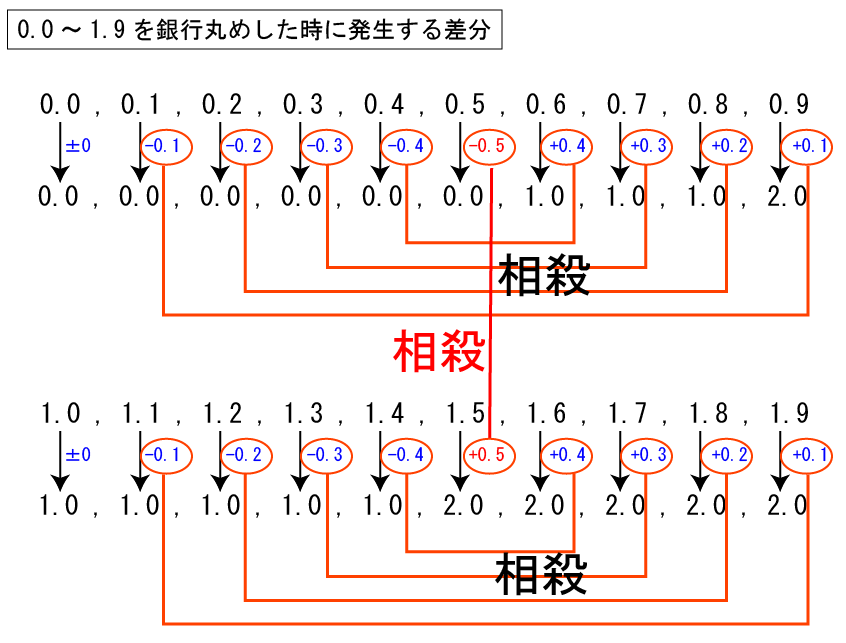
0.0から1.9を整数に丸める例で考えます。0.0か2.0のどちらかになります。
0.5は切り捨てられて0になります。1.5は切り上げられて2になります。この2つが相殺になるため、ランダムな数値ではトータルで±0になることが期待できます。
銀行丸めのやり方
0.0から10.0を銀行丸めで整数にする場合で説明します。
計算方法の違いは0.5を含む場合の扱いです。
- 0.5がなければ四捨五入と同じ
- 0.5を含む場合は、結果が偶数になるようにまるめる
具体的には下記の赤文字の場合に通常の四捨五入とは異なることになります。
0.5 → 0
1.5 → 2
2.5 → 2
3.5 → 4
4.5 → 4
5.5 → 6
6.5 → 6
7.5 → 8
8.5 → 8
9.5 → 10
なぜ銀行丸めだと誤差が小さくなるのか
先に書いた通り、四捨五入の場合に切り捨てられる値の平均は -0.25、 切り上げられる値は平均+0.3です。
銀行丸めの場合、1.1, 1.2, 1.3, 1.4は四捨五入と同じ計算なので平均-0.25。
1.6, 1.7, 1.8, 1.9の4つの場合に2になるので
切り上げられる値は +0.4, +0.3, +0.2, +0.1で 平均+0.25。切り捨てと同じ値です。
そして1.5, 2.5, 3.5など[整数+0.5]の場合は
[奇数+0.5]になる確率、[偶数+0.5]になる確率次第ですが、これはどちらも50%です。
言い換えると、+0.5になる確率と-0.5になる確率が同じなので究極的には±0です。
そのため、四捨五入の場合よりも誤差が小さくなることが期待できるわけです。
実際の計算結果例
ランダムな数値を50個作り、実際に比べてみました。
3.4
7.8
2.1
5.7
9.2
4.5
6.1
1.9
8.3
2.5
4.9
7.2
3.8
6.4
5.1
1.6
9.5
2.3
4.7
8.1
5.3
7.6
3.1
6.9
2.7
4.3
8.6
1.2
5.9
3.7
7.4
6.2
2.9
8.4
1.5
9.1
4.6
7.3
3.9
5.8
6.5
2.4
8.2
1.8
7.9
4.1
5.4
2.6
9.7
3.2
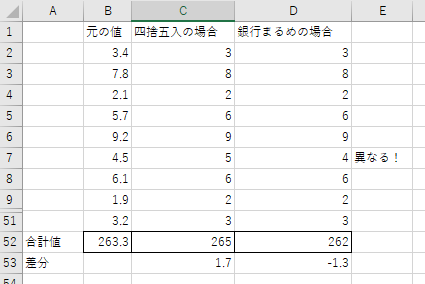
行数が多いので、下図は10行目から50行目までを非表示にしています。
元の値の合計値との差分を比べてみると、四捨五入は+1.7、銀行丸めは-1.3
銀行丸めの方が差分が小さいことが分かります。
まとめ
今回の例でまとめると、銀行丸めの特徴は
- 0.5を含まない場合、切り上げと切り捨ての誤差は同じ
- 0.5を含む場合は、+0.5になる確率も-0.5になる確率も50%なので誤差は(究極的には)0に近いことが期待できる




コメント