中学校で習った一次関数からスタートしてAIの基本を紹介します。生成”ではない方の”AIです。
レベル的には、データサイエンスを学び始めるとよく見かけるアルゴリズム、またG検定に出てくる基本的な用語をおさえるレベルを想定しています。
データ分析がAIの第一歩
例えば下図のような身長と体重のデータがあったとします。
身長に応じて体重も重くなる傾向があり、このようなデータを相関関係ありと言います。
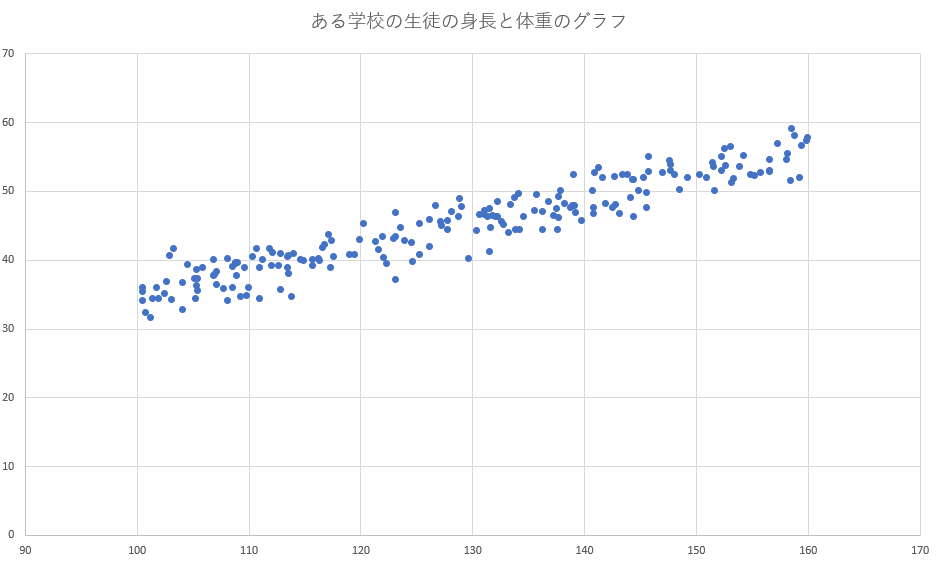
相関関係が見られる場合、下図のような直線が直感的に想定できると思います。
直感ではなく数学的にこれを求める手法を回帰分析と言います。
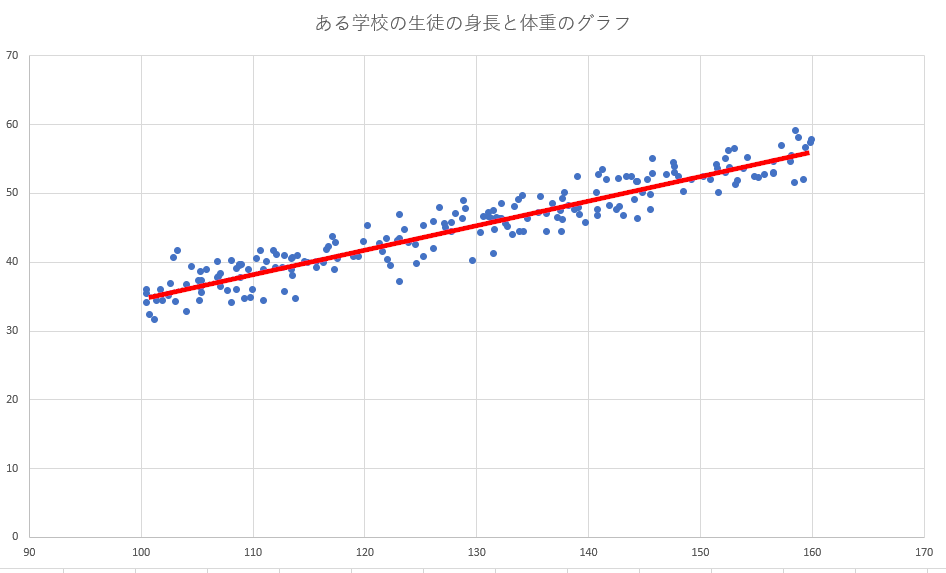
直線のグラフは中学校で習った通り y = ax + b です。
回帰分析でこのaとbを算出すれば、先ほどの図の赤線が求められます。
エクセルの回帰分析機能で計算したところ
y = 0.3524x – 0.3376
と算出することができました。(この算出方法は後で紹介します。)
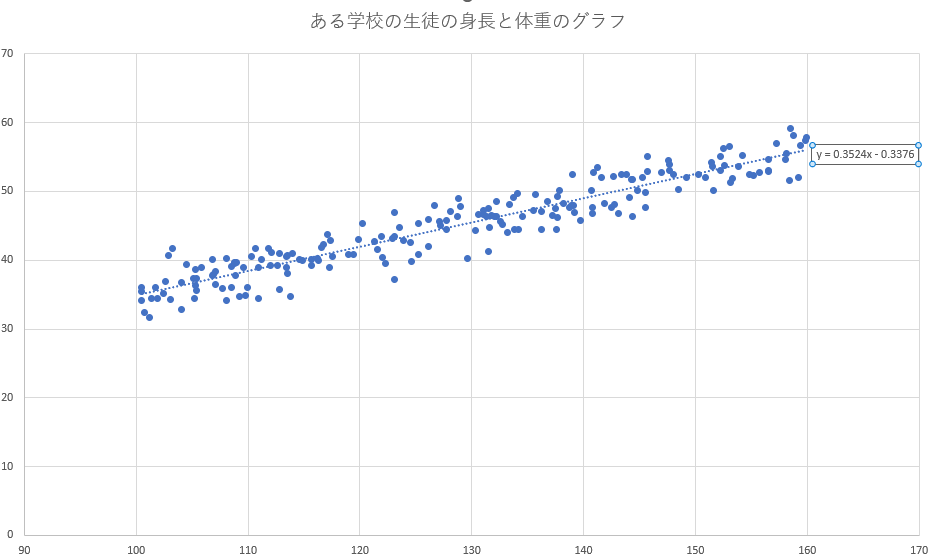
この y = 0.3524x – 0.3376 から
「この集団に身長90cmの子がいたら、その子の体重は31kgくらいではないだろうか」
と推定することができます。
このような推定を「AIによる予測」と呼んでいる訳です。
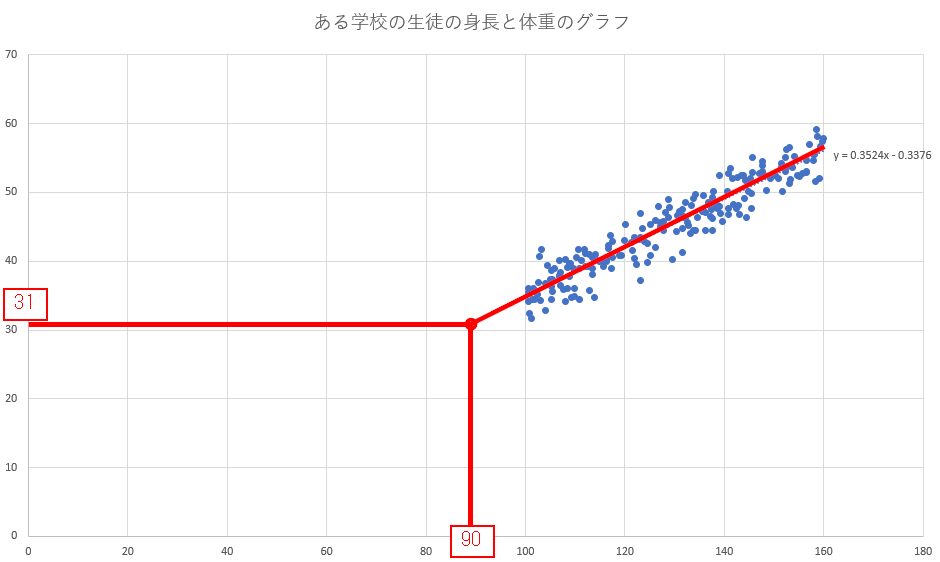
ちなみに90cmで31kgとはかなりの肥満ですが、それは大人と子供の体格の差を考慮できていないためでしょう。
これは今回の線形による単回帰分析での精度の限界といえます。
この精度を上げるために考えられる方法ついては、後ほど重回帰分析、非線形解析をご紹介します。
エクセルで回帰分析をしてみる
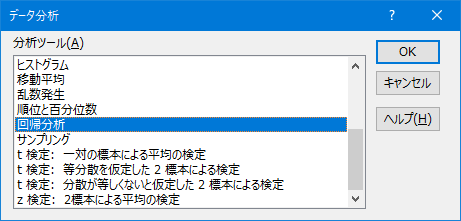
エクセルの「分析ツール」を表示させる
下図のように「データ」-「データ分析」が見えていれば大丈夫です。

見えていなかったら、エクセルの「ファイル」-「オプション」から「アドイン」-「設定」で「分析ツール」にチェックを入れてください。
詳しくは「エクセル 回帰分析」などで検索したらツールの出し方を説明してくれているサイトが見つかるでしょう。
エクセルの回帰分析ツール
早速、分析ツールを使ってみます。
A列とB列には、チャットAIで適当に作ってもらった身長と体重の200人分のデータが前もって貼ってあります。

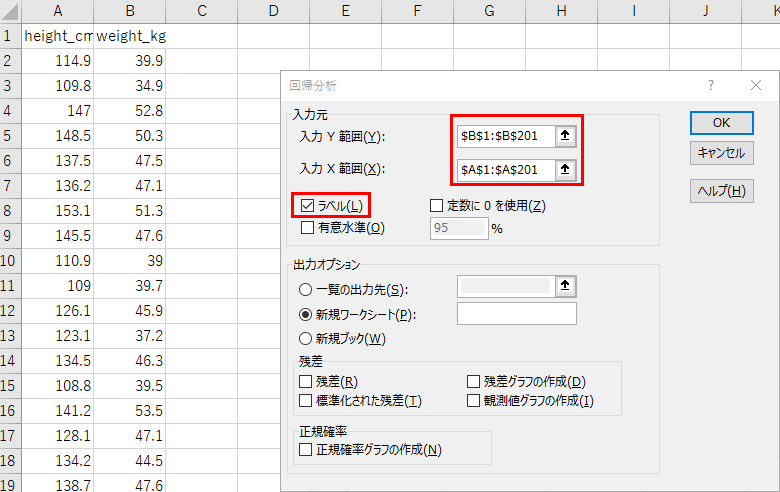
上の例では出力オプションが「新規ワークシート」なので新しいワークシートに分析結果が出ます。
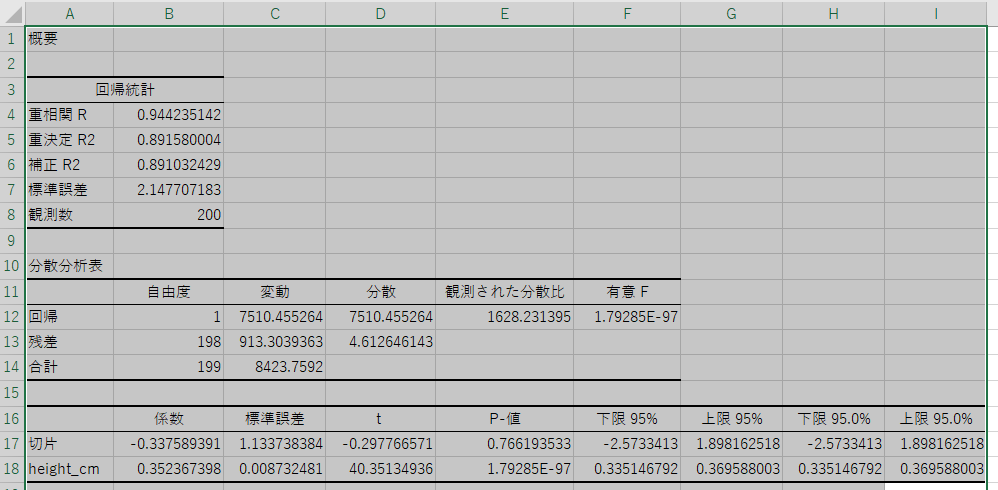
この各用語や数値の意味に興味があったら、統計検定2級、または統計検定のデータサイエンスで学ぶことができます。
次に散布図と近似曲線を描いてみます。
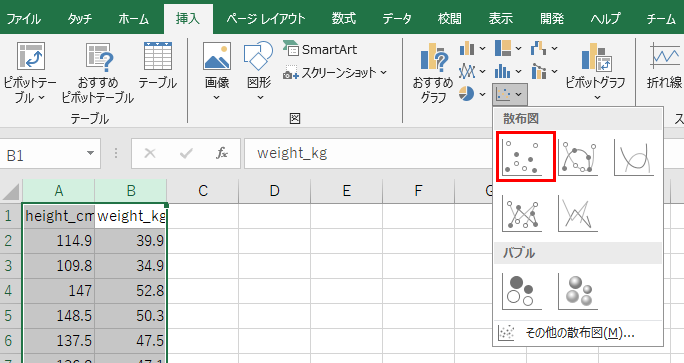
散布図が描けました。
左と下にあまりにも空きがあるのでx軸、y軸それぞれの最小値を調整します。
解析をさせるには、「+」ボタンを押します。
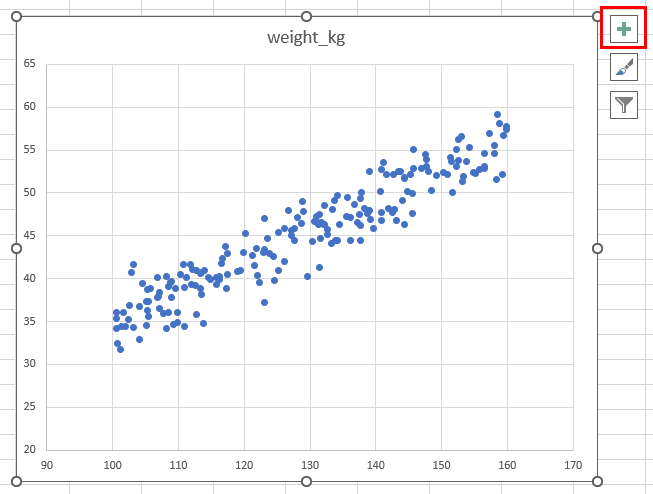
今回の例では「近似曲線」の「その他のオプション」を選びます。
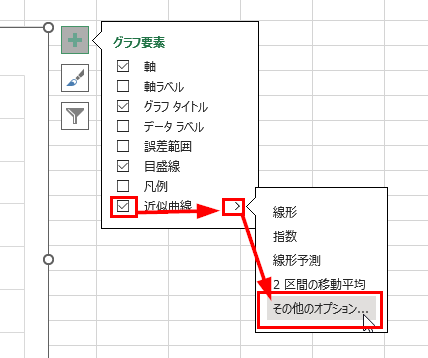
「グラフに数式を表示する」を選択すれば、このグラフの近似曲線の数式が表示されます。
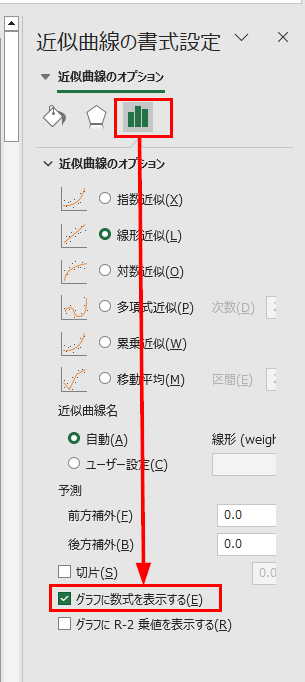
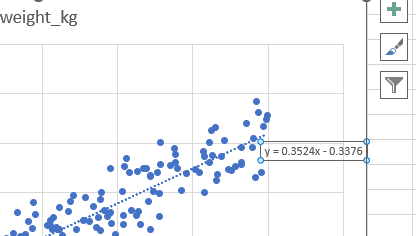
この直線を表す y = 0.3524x – 0.3376 と表示されました。
回帰分析の種類
単回帰と重回帰
今回の例で紹介した手法は、目的変数(体重)に対し説明変数が一つ(身長)なので単回帰分析といいます。
ところで先ほど、サンプルデータから身長90cmの時には体重31kgと予測がでました。
かなりの肥満です。
これは、大人と子供の標準体重が加味されてないことが原因なので、たとえば性別、運動歴、年齢など情報を増やすと予測精度が上がると考えられます。
単回帰分析よりも説明変数を増やしたものを重回帰分析と言います。
特徴量エンジニアリング
本当に人間のように何でもできる汎用AI(AGI: Artificial General Intelligence)はまだ開発されていません。
そのため、作成したAIの精度を上げるために他のアルゴリズムを試したり、学習データに変更を加えることがあります。
特徴を顕著なものにしたり正規分布に近づけるために学習データに手を加えることを特徴量エンジニアリングと言います。
また、特徴量と似た用語に説明変数があります。
説明変数は「統計学、回帰分析」の分野で使う用語、特徴量は「機械学習、AI」の分野で使う言葉です。
どちらが登場するかは文脈次第ですが、意味するところは同じと思って大丈夫でしょう。
連続値とカテゴリ値
今回の例では身長や体重という連続値の分析をしていますが、カテゴリ値に有効な線形解析のアルゴリズムにロジスティック回帰が挙げられます。
カテゴリ値とは犬/猫、故障/正常 のような数値ではない値のことです。
回帰分析以外のアルゴリズム
回帰分析だけではなく、目的によってアルゴリズムを使い分ける必要があります。
その他の分析手法もご紹介します。
線形と非線形
ところで、先に紹介した身長と体重の例がもし一人の子供の成長記録としたらどうでしょうか。
全体として右上がりなのは当然なので、どちらかといえば次の数値が上がるのか下がるのかが重要になります。
下図のような折れ線グラフが、次は上がるのか下がるのか。
この場合は線形分析(直線)とは違う分析の方が適しています。
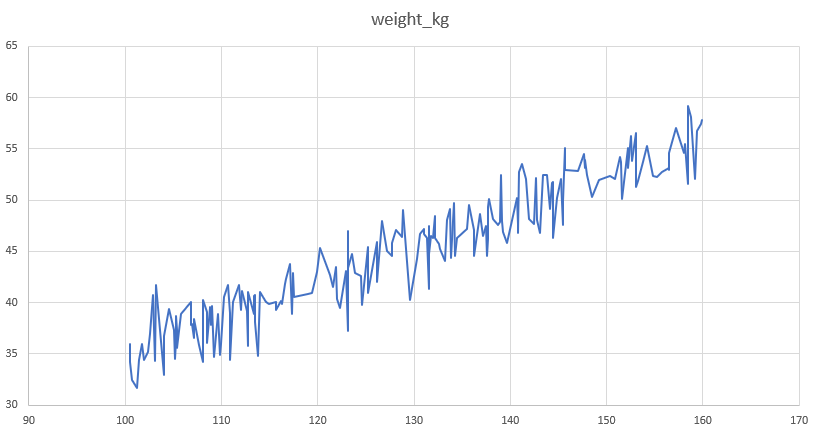
非線形モデルには決定木(ディシジョンツリー)があります。
例えば問診のように「体温は何℃?」「咳は出る?」などデータの枝分かれ具合(説明変数)を分析・学習することで、そこにないデータの人を風邪をひいているかどうかを予測するイメージです。
過学習というデメリット
非線形モデルで考えるとデータに含まれる条件を詳しく分析・予測することができる反面、学習データに適合しすぎると未知のデータにはむしろ弱い状態になってしまいます。
過学習という現象で、「学習データほど体温が高くないケースはすべて『風邪ではない』」とみなしてしまう具合です。
アンサンブル
予測精度を上げるための工夫としてAI同士で多数決をさせる手法をアンサンブルと言います。AIでも多数決をすると予測精度が上がりやすく、そのアンサンブルのアルゴリズムもまた色々考案されています。
アンサンブルの考え方
アンサンブルについては「Kaggle Ensembling Guide」という記事の説明が分かりやすくて有名です。
詳しく知りたい方はそちらを参照してください。
ここでは70%の精度の分類器(A,B,C)で解析する例で説明します。
①3つとも正解を出力する確率
0.7 × 0.7 × 0.7 = 0.343
②2つが正解を出力する確率
(0.3 × 0.7 × 0.7) + (0.7 × 0.3 × 0.7) + (0.7 × 0.7 × 0.3 ) = 0.441
③1つだけが正解を出力する確率
(0.3 × 0.3 × 0.7) + (0.3 × 0.7 × 0.3) + (0.7 × 0.3 × 0.3 ) = 0.189
④3つとも不正解を出力する確率
0.3 × 0.3 × 0.3 = 0.027
このA, B, Cで多数決をしたアンサンブル結果は
0.343 + 0.441 = 0.784
で78%の正解率となり、単体の70%よりも正解率が高くなったことが分かります。
アンサンブルの手法 バギング
複数の学習モデルの予測結果から「平均」や「多数決」で統合して予測値を出すことをバギングと言います。
ランダムフォレストのアルゴリズムでは内部的に複数の決定木モデルを持ちバギングを行い、決定木単体よりも高い精度を出すことができます。
アンサンブルの手法 ブースティング
学習をさせる中で重みをつけ(ブーストをかけ)ます。
これにより性能が低い学習器であっても精度の高いモデルを構築することができます。
勾配ブースティングのアルゴリズムでは内部的に複数の決定木モデルを持ちブースティングを行い、決定木単体よりも高い精度を出すことが出来ます。
コンペで上位順位者に人気のあるXGBoost や Light GBMも決定木のブースティング系アルゴリズムです。
アンサンブルの手法 スタッキング
異なるモデルの結果をまとめてさらに別のモデルで最終予測をすることをスタッキングと呼びます。
類似しているモデル同士よりも、系統の異なるモデルを扱った方が高い精度が出やすいようで、イメージ的には、得意分野に特化した専門家の意見を持ち寄るイメージと言えるでしょう。
まとめ
アルゴリズムは日進月歩でどんどんいろいろなものが考案されています。
そういう点でAIの作り方に唯一の正解というものはなく、あるのは開発者達の地道な工夫です。
アルゴリズムを駆使してデータの分析をする事をデータサイエンスと言い、分析結果から設計された分類機を実行する仕組みがAIと呼ばれます。


コメント