前回、エクセルで平均律の周波数を計算してみました。音は空気中を伝わる波の振動で、そして波は正弦波で表すことができます。正弦波はサインカーブとも言います。今回は音である正弦波をExcelでグラフ化してみます。周波数を可視化してみるわけです。
ラジアンを使うと何が嬉しいのか
三角関数といえば、高校で三角関数を習う時にいきなり「ラジアン」が出てきて当時私は悩みました。
「小学校で0°~360°と教えていたくせに。面倒な計算をさんざんやらせたくせに。何をいまさら『あれは使いません』的なことを」と(笑)。
小中学校の時、角度を表すには度数法でした。30°とか90°とか。
そして「円弧の長さを求めなさい」なんて問題が出題されると
「直径×3.14× [360分の角度] …」なんて面倒な計算をやったもんです。
半径と中心角から弧の長さを計算するのではなく、逆の発想で
半径と弧の長さが等しい時の中心角を1ラジアンと呼ぶことにしたのが弧度法です。
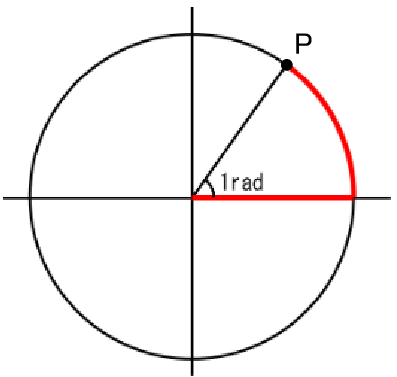
円弧の長さを基準にしたので、角度と半径を手掛かりにして円弧を計算する必要がなく
また、点Pの位置を知りたいときはcos、sinでX座標とY座標も出すことができます。
ここでは説明を省略しますが、波はsinカーブで描くことができます。
Excelで正弦波を可視化する
まず連続データで角度の数値を作ります。さしあたり0~720°とします。
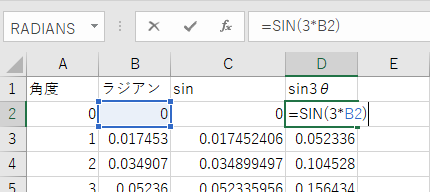
そしてRADIANS関数を使って角度を度数法(°)から弧度法(ラジアン)に変換。
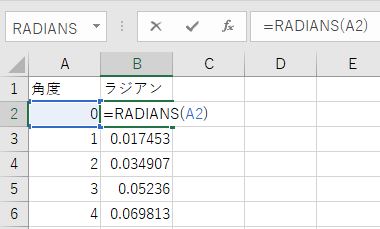
SIN関数を使って基本周波数のsin波の値を作る
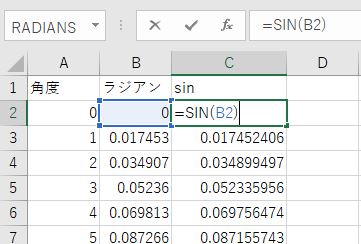
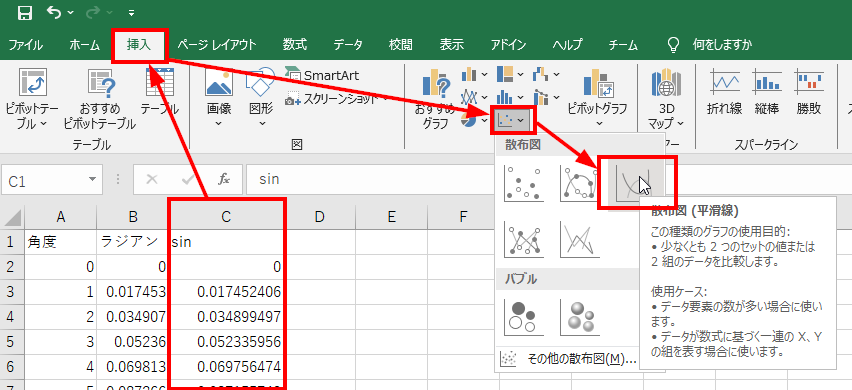
C列を選択し、散布図としてプロットするとグラフ化できます。
仮にこれが1秒間の波だとしたら、1秒間に2往復の振動をする2Hzの波形です。
sin関数の中を3倍にしたらy = sin 3θの正弦波になります。
仮にこれが1秒間のデータとしたら6Hzの波です。
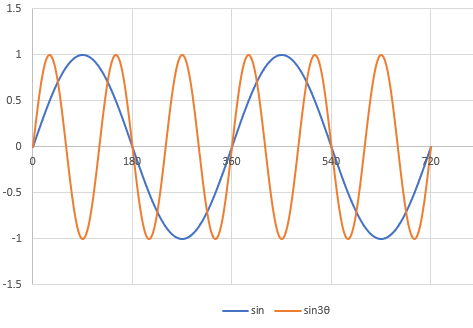
それにしても重ねた音に、協和音、不協和音という区分があるのはなぜでしょうか。
次回は和音を可視化してみます。
次回、これを可視化してみることで協和音とは何かを見ていきます。





コメント