私は学生時代、音楽の授業が苦手で嫌いでした。音階というルールそのものの普遍性が分からないというか、根拠が分からないというか。ただ逆に、そんな音階の理屈が実は物理・数学的だということを知ってからは興味が湧きました。自分の理解した経緯に沿って、エクセルでその周波数を計算する方法を紹介します。
１オクターブという区切り
あるとき、友人にバイオリンを触らせてもらったことがあり、そのときに
弦の長さを半分にすると一オクターブ上の同じ音が出るということを知りました。
逆に言えば、弦の長さを半分にしたときに出る音を”１オクターブ上の同じ音”と呼ぶことにした、と言えるのかもしれません。
そしてこれはバイオリンに限らず、すべての弦楽器は同じことがいえます。
なぜなら、物理現象として
弦の長さが1/2 = 周波数が2倍
弦の長さが2倍 = 周波数が1/2倍
なので、周波数が2倍になった時の音を”１オクターブ上の同じ音”と呼ぶことにしたと言えるからです。
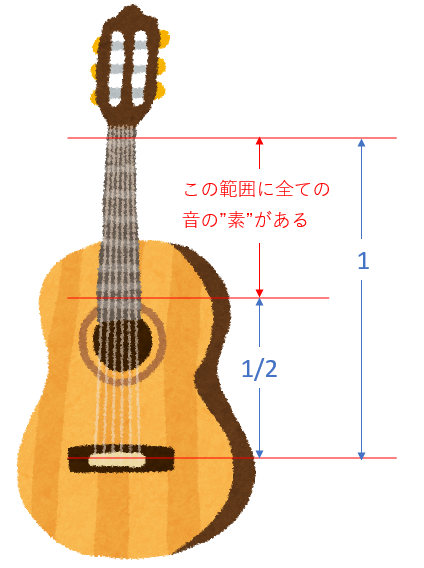
1の長さと1/2の長さの間に全ての音の”素（もと）”がある。
押さえる位置は無限通りあるので、音の素も無限にあります。
となればあとは、どういうルールでデジタル化（数えられる形）にするか。
つまりオクターブという区切りを知り、その区切りの中をどう区切るのかが音階だということが分かってきました。それを考えた人がいたようです。ピタゴラスの定理で有名なピタゴラスさん。
ピタゴラス音律とは
ピンと弦を張る力と、その弦を抑える腕の長さと力があるなら、究極的には一本の弦であらゆる音階が出せるということになります。実際、ピタゴラスは1弦琴で実験をしたそうです。
弦楽器は普通、異なる太さの弦を複数本持っていますが、それは実用上の理由なのではないでしょうか。これもまた自分には目から鱗でした。
ピタゴラス音律の比率をエクセルで計算する
ある音を基準1としたときに1～2の間を一つのオクターブと呼ぶことにしました。2倍の音は１オクターブ上の音、1/2の音は１オクターブ下の音です。そこで異なる音を集めるため、2や1/2ではなく3を使ってみます。1とか2、1/2というのは音の比率です。具体的には音の周波数の比率です。
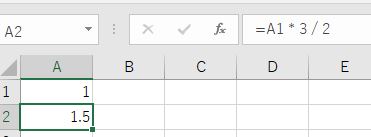
① 基準にするの周波数を1とする
② その3倍を求める
③ 計算結果が2を超えてしまっている場合は、注目しているオクターブに納めるために1/2倍する
④ この結果2を超えていればさらに③へ（つまり1/2倍する）
超えていない場合は⑤へ
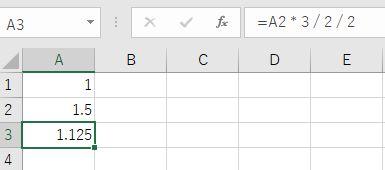
⑤ もともとの1と同じ数値に戻ったら計算終了
これを繰り返すと7回目に1.06で近似します。
小さい順にソートしなおして名前を付けたら、ドレミファソラシと同じ7音＋１オクターブ上のド。
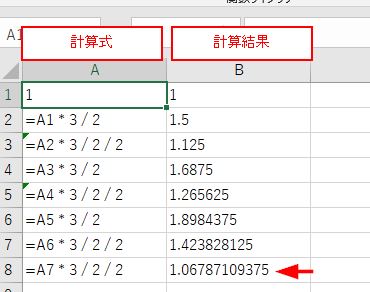
8音でソートせずさらに繰り返すと12回目に、先ほどよりも誤差が小さい1.01で近似します。
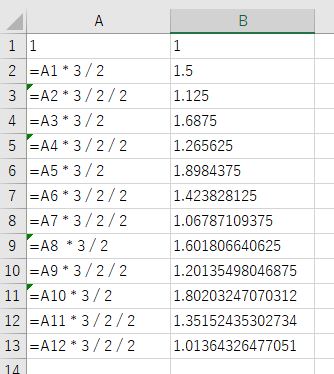
これを小さい順ソートして名前を付けたら
ド、ド#、レ、レ＃、ミ、ファ、ファ＃、ソ、ソ＃、ラ、ラ＃、シと同じ12音＋１オクターブ上のド。
ピアノの黒鍵と白鍵の音たちと同じ数です。
ピタゴラス音律の周波数に換算する
音楽の世界で基準となるのはラ（440Hz）だそうです。それを基準にして具体的な周波数を計算してみます。
まず一連の計算を「ラを1とした比率」に換算します。ここでは周波数比率と名付けました。
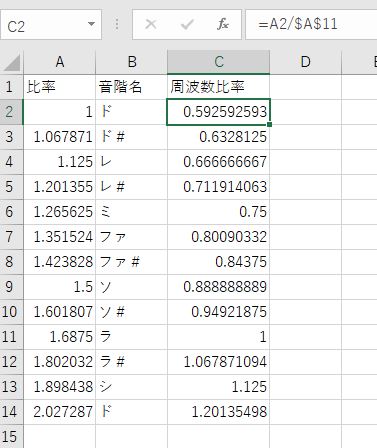
それに440を掛け算したら、ラを440Hzとしたときの各周波数がでます。
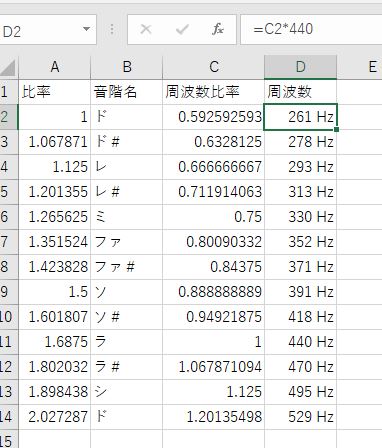
計算結果から次の課題が見えてくる
ところでこの周波数の差を見ると、0.06から0.11まで2倍近い開きがあり、意外とムラがあることが分かります。
こうなると「12個ありき」を前提にして平均的に12分割したくなります。
これが「平均律」ですが、そこは次の機会にして今回はここまで。
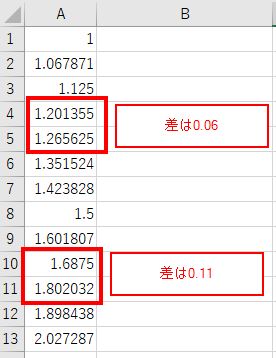
まとめ
周波数が2倍になった時の音を”１オクターブ上の音”と決め、その中に入る音を下記の要領で算出したのがピタゴラス音律です。
- 440Hzを基準として、これに対し3倍の法則にある周波数を集めた
- 計算が進んで元の値に近似（1.01）したところで計算終了
- 実際に計算をしてみると意外とムラのある分布である
最後まで読んでいただきありがとうございました。
コメント