【Excel】平均律をエクセルで計算する

ピタゴラス音律を実際に計算をしてみると、その周波数同士の比率に結構ムラがあることが分かりました。すると平均的に分割したくもなります。これが「平均律」です。今回はこの平均律をエクセルで計算する方法を紹介します。

私は学生時代、音楽の授業が苦手で嫌いでした。音階というルールそのものの普遍性が分からないというか、根拠が分からないというか。ただ逆に、そんな音階の理屈が実は物理・数学的だということを知ってからは興味が湧きました。

平均律とは
Excelで〇乗を計算すると平均律が計算できる
余談：1オクターブ53音階
まとめ

平均律とは

ピタゴラス音律は、音階同士の差に結構な違いがありました。ムラがあるといえるかもしれません。
平均的に12分割をするという発想は、さもありなんという感じがします。
そしてこの発想が西洋クラシックの基本になっているようです。

オクターブを分割するにあたっては、ただの掛け算や割り算では出せないことに要注意です。
周波数2倍、4倍、8倍…という乗算の関係にあるからです。

1つ上のオクターブは、周波数2倍（2倍 × 1）。
2つ上のオクターブは、周波数2倍の2倍（2倍 × 2倍）で4倍。
3つ上のオクターブは、周波数2倍の2倍のさらに2倍（2倍 × 2倍 × 2倍）で8倍。

ちょっと余談になりますが
1,2,34,8,16,32, 64, 128, 256, 512, 1024, 2048…
あっという間にすごい桁数になる上に数値が飛び飛びで扱いが大変。
その点は対数を使えば1,2,3,4…と扱えます。
2倍は log₂ 2 = 1
4倍は log₂ 4 = 2
8倍は log₂ 8 = 3
16倍は log₂ 16 = 4

さて、逆に分割する場合を考えます。
例えば12分割なら「12回掛け算して2になるもの」。2の12乗根です。書き方は¹²√2 または 2^1/12。

Excelで〇乗を計算すると平均律が計算できる

「〇乗」をエクセルでは ^ を使って表します。2の12乗は2^12と表し、2の12乗根なら2^(1/12)。
平均律の、1に12回掛け算したら2になる区切りは 2^0/12から2^12/12まで計算することで計算できます。

2の0/12乗～2の12/12乗
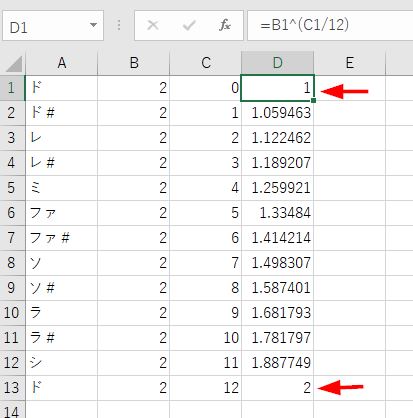
最上段は2の0条なので１、最下段は2の12/12乗なので2になっています

この周波数比率をもとに　ラ=440Hzで換算すると、平均律の周波数が計算できます。

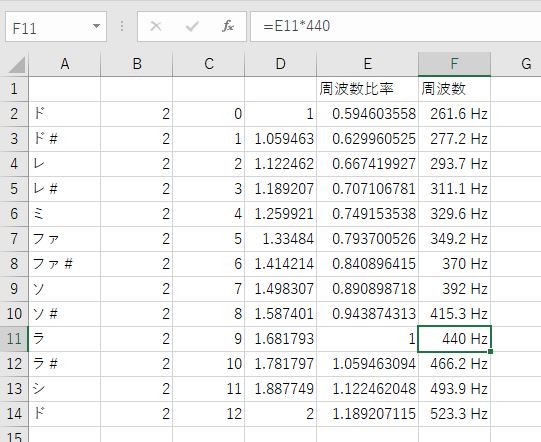
ところで、平均律は分割の均等な反面、ずらしたことにより正確な響きが良くないようです。
倍音ではなく理論値でずらしたズレが理想的な共鳴にならないからです。

これへの対応として２つの方向性が考えられます。
１．12分割がそもそも正しかったかどうか
２．12分割はひとまず前提としたうえで響きをよくするにはどうしたらよいか

余談：1オクターブ53音階

田中正平という方をご存じでしょうか？
12分割が正しかったのかを疑って発想をした人で、独自の音階で1オクターブ53音階のピアノを作りました。どういう理屈で53音階になったのかは、ピタゴラス音律の際に紹介した計算を続けると想像できるような気はします。

前回のように計算をすると
8音階（誤差0.068）からさらに計算を進めると、12回目に（誤差0.014）が現れますが
12音階（誤差0.014）からさらに計算を進めると、53回目に（誤差0.002)が現れます。53音階です。この53が田中正平さんの53音階の元になったと思います。

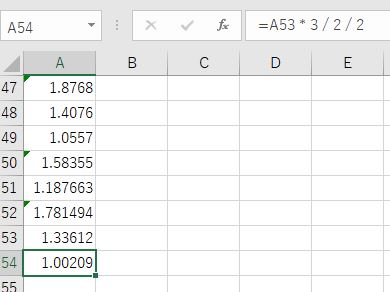
ピタゴラス音律と同様の計算を53回計算を繰り返した54行目に
1.002という、1に限りなく近似した数字が表れる

この発見がもっと早くヨーロッパあたりで起きていたら、もしかしたら今頃、ピアノの１オクターブは53鍵盤が普通になっていたかもしれないですね。そんな想像を掻き立てられます。
逆に、12分割をひとまず正としたうえで対応を考え直す方向性は純正律と言います。

まとめ

まず3倍音を集めたピタゴラス音律ができました。しかし周波数の区切りが一様ではないので、「12分割ありき」の前提で平均的に区切る試みがありました。これが平均律です。
次回はExcelで数値計算した平均律をグラフで可視化します。

【Excel】周波数をエクセルでグラフに可視化する

前回、エクセルで平均律の周波数を計算してみました。音は空気中を伝わる波の振動で、そして波はサインカーブで表すことができます。今回は音であるサインカーブをExcelでグラフ化してみます。周波数を可視化してみるわけです。

理論で12分割をしたことで実際の倍音とはズレが生じて共鳴が悪くなってしまう問題がありました。
そこで今度は、平均律の値に近い倍音を組み合わせる動きがありました。3倍音だけでやるとピタゴラス音律に戻ってしまうのですが、3倍音だけでなく5倍音など他の倍音も使うことで、あくまで倍音を使いながらも平均的な区切りを実現した。これが純正律です。

最後まで読んでいただきありがとうございました。