子供のころ算数が苦手で何度も躓きました。「算数なんて人生で何の役に立つのか」と子供ながらに感じていました。しかし逆に、数学の苦手意識を乗り越えられのたはそれらつまずきのお陰でもあります。何度もつまづいたからこそ理不尽に思った事が印象に残り、後から考えるきっかけになったからです。
子供が算数で躓いているとき、「なんで分からないの!」なんて頭ごなしに言うのではなく、実は小学校の算数は難しいということを知っておいてあげるのは重要だと思います。
0.00000…1 =0? それとも0ではない?
私は小学校で比例と反比例を習ったとき
「反比例のグラフは、右に行くにつれて0に近づくけど0にはなりません。分かりましたか?」
と先生に言われました。私だけ納得がいかずに「ちょ、ちょっと待って…」と、しばらく考えました。
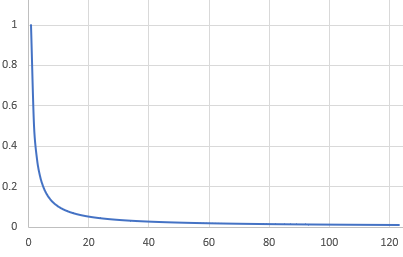
だんだん0に近づくのにいつまでも0にならないなんて
「0.1、0.01、0.0001、0.000000001、…。そうか0001の0が増えるだけなら0にはならないのか」
という考えに至ってようやく納得できました。
それにしても、「どこまでいっても0が増えるだけで、いつまでたっても0には到達しない。」って、ゼノンのパラドックス(※)すら想像させます。
※「先を走っている亀に、アキレスは決して追いつけない。なぜならさっきまで亀がいた地点にアキレスが到着した時、亀は既にそこより少し先に常に進んでいるから」というやつです。
そんなパラドックスみたいなことを「分かりましたか?」だけで教わるなんて、小学校の算数ってつくづく難しいと思います。
しかも当時はそれで納得したものの、今なら
「0.0000000000…1って、やっぱり0じゃないですか?先生。」と反論してしまうところです。
0.33333333… = 1 ÷ 3 は正しい。
両辺に3を掛けると
0.99999999… = 1
両辺それぞれを1から引くと
1 – 0.99999999… = 1 – 1 つまり
0.00000000…1 = 0
もし当時ここまで思いついていたら私は先生に「分かりました」と答えられなかったでしょう。小学校で習うことを納得するのってある意味、高校の授業よりも難しいのかもしれない。
掛け算と割り算を先に計算するって、何のため?
掛け算と割り算を先に計算するとか、( ) も先に計算するとか
計算を複雑にするだけのようなそんなルールも納得できませんでした。
中学に入って「×(掛ける)は省略する」と教えられたときには、式が何を言っているのかも分からなくなる感覚でした。何通りにも読めそうなものをどう読めばよいのか分からない、というか。
例えば 10xy÷2xy = って本当に答えは5?
式の読み方によっては5y2 だったり5x2y2 だったりするよね?
みたいな。
ちなみに 6÷2(1+2)=?という有名な問題があります。
計算機やパソコンのソフトによっても答えが分かれるし、数学者でも答えが分かれるんだそうです。
だから言ったのに(言ってない笑)
私はこの辺りの専門家ではないので興味があったら詳しい説明はググってみてください。
数学の苦手意識克服のきっかけ
そんな自分ですが、友人と音階について調べごとをしたとき、平均律の理屈を友人に説明することになりました。対数とか212/12を再度復習したのをきっかけに今更ながら数学の理解が深まりました。ラジアンもそうです。


数学って「なにかしら便利さが生まれる工夫」のはずなんですよね。そして何のための工夫なのかという「その定理の目的」を知ることが大事なんだと気づきました。その目的を見つけて友人に教えてみたのもまた良かったようです。人に説明をしてみるって一番の勉強法だと思います。
さらに「でも、まだこういうときにおかしい気がするんだよな」と
相手になったつもりで反論してみると、さらに一段理解が深まります。
上で紹介した、「0.00000…1 =0? それとも0ではない?」とか
「掛け算と割り算を先に計算するって、何のため?」のように。
練習問題、発展問題、チャレンジ問題など、できない壁にぶち当てるのが目的なのかと思ってしまう受験勉強では得られなかった視点でした。
まとめ
- 子供の頃の数学嫌いは後から克服できる
- 数学は何かの役に立つから教えられるもの。「何の役に立つんだろう」と考えてみるのも面白い
- 人に教えてみる
最後まで読んでいただきありがとうございます。


コメント