前回、sinθとsin2θ の波をグラフ化してみました。
今回は”響きが悪い”と言われる平均律の音律を、Excelで見える化して検証してみます。
音のサイン波をグラフ化する
グラフの作り方は前回と同じ要領です。
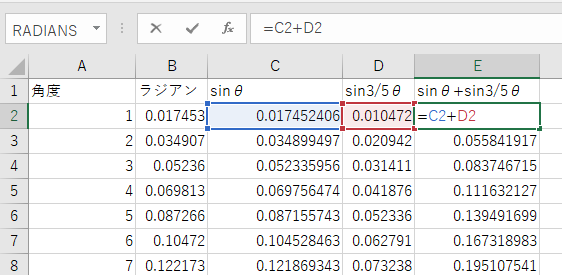
- 3600°までの値をA列に作る
- B列にradian関数を入れ、A列をラジアンに換算する
- C列にsin関数を入れ、B列のラジアンをsinにする
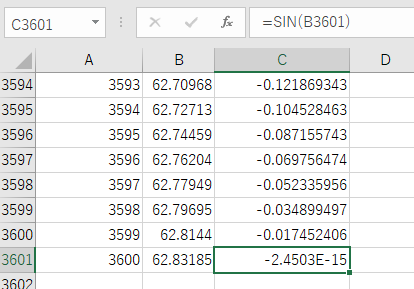
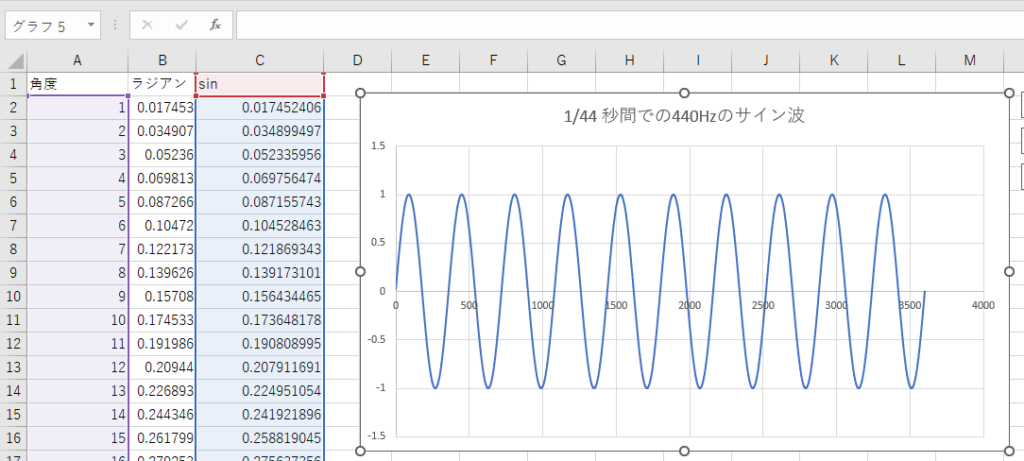
あとはこの10個の山のグラフをどう見るかです。例えばラの音は440Hzなので、1秒間に440個の山ができます。
1/44秒間の出来事とみなせば、この10個の山のグラフは「ラの音のグラフ」と見なせます。
純正律と平均律のド・ラを可視化してみる
響きが良いという純正律で、協和音と言われる組み合わせ「ド・ラ」を合成してみます。
純正律の周波数比率は別途Webで調べました。ド=1としたとき、ラ=5/3。ということは、ラ=1としたらド=3/5です。
ラ=440Hzに対しド=264Hz。
sinθに対し、sin(3/5)θを作ってグラフにしてみました。
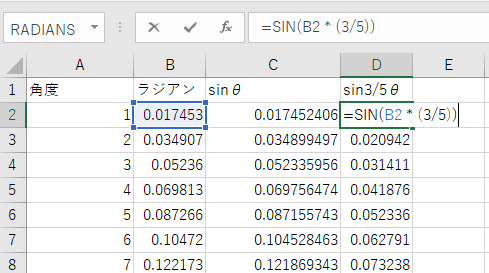
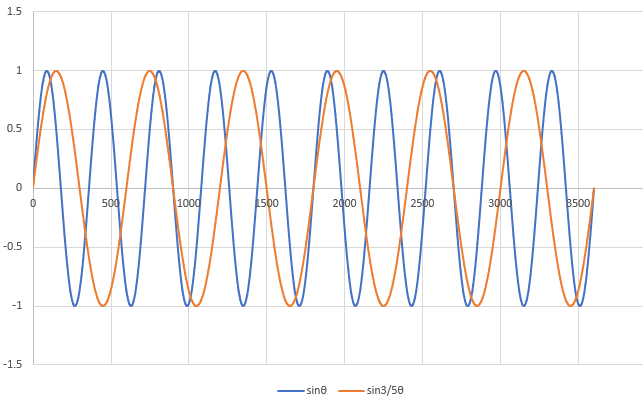
純正律「ド・ラ」の和音を可視化する
和音の形を見るために足し算してグラフ化してみます。
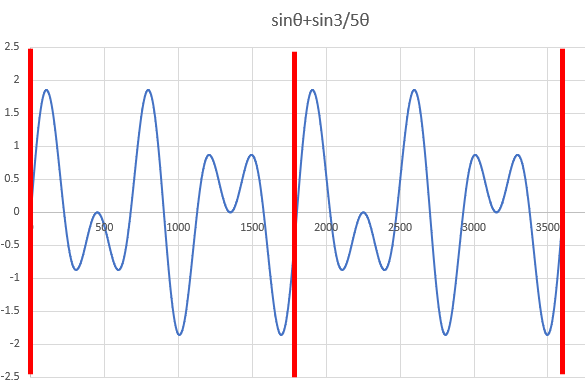
これが良く響くという純正律による和音「ド・ラ」です。赤い縦線の間を1周期とした、2周期の波になりました。この横軸全体が1/44秒なので、1/88秒で繰り返す秩序と言えます。
平均律「ド・ラ」の和音を可視化する
比較対象がないとピンとこないので、平均律の和音「ド・ラ」も見てみましょう。
平均律の比率は前回算出した数値から、ラ=1のとき、ド=0.594です。純正律が3/5(0.6)だったので、少しズレがあります。
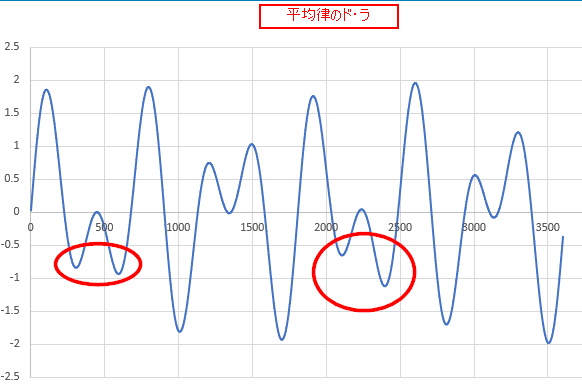
グラフにしてみると、なるほど純正律ほど美しくありません。
…と言うのは赤丸の箇所にまだ違いがあり、この1/44秒間ではまだ波形が安定していないからです。
この波形が安定したとき、よく響く音とか美しい響きというんだと思います。
さらに横軸を広くしてみても、なかなか安定した繰り返しになりません。
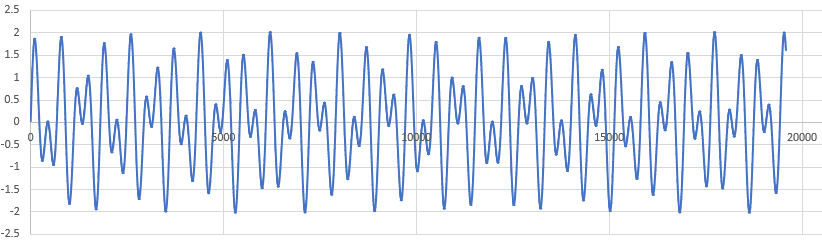
これは実際の響き方も安定していないと言えそうです。これが「響きが悪い」と言われる所以ではないでしょうか。
音感のある人には、聞いたら明らかなのかもしれませんが、このグラフからは音感がなくてもそれが理解できる気がします。
平均律は和音の周波数が安定せず、いわゆる「響きが悪い」状態。これを安定して響かせるためにシンプルな比率にしたのが純正律ということでしょう。
まとめ
協和音「ド・ラ」を題材にして純正律と平均律を可視化してみると、純正律は短い周期で「繰り返し」になることが分かりました。音が短時間のうちに安定するということが、人間に取って心地良い響きと言えそうです。



仮説
ここでは扱いませんでしたが、不協和音のグラフも面白そうです。
不協和音=聞き苦しい音ということではないようで、その音の不安定さから不安感の演出に効果的だったりします。
何はともあれ仮説としては
「不安をあおるような効果あり」=「和音の波形がなかなか安定しない形」となるのかもしれませんね。



コメント