サインコサインタンジェント、数学が苦手、嫌いな人には嫌悪感を感じさせる響きがあるようです。中学生の知識での再入門を紹介します。中学生の知識での再入門とはいえ、伊能忠敬が富士山の高さを測った方法もこの方法ですから、決して子供騙しでも役に立たないものでもありません。
三角形の辺の長さを知りたい時の方法
直角三角形では2辺が分かれば残る1辺も分かります。ピタゴラスの定理です。
直角三角形以外にも使えるのが三角関数です。ここでは説明のため直角三角形で考えます。
下の図で a:b:c = a:b:c という比が成り立ちます。例えば具体的に、赤い三角形の3辺が5cm, 4cm, 3cmで、青い三角形のaが10cmだったなら、残る2辺は8cmと6cmです。
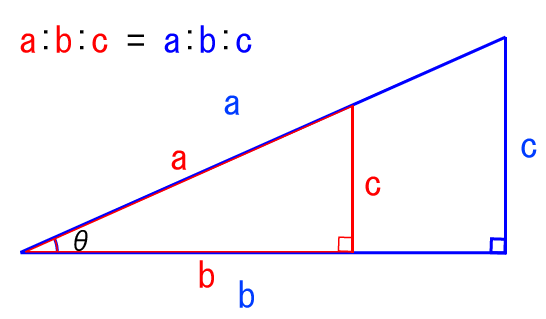
2つの比で見ても同じです。a:b = a:b などなど、などなど。
比は分数でも書けます。a/b = a/b などなど、などなど。
どの組み合わせでも良いのですが、例えばcとaで見てみます。
c/a = c/a この分数を変形すると
c = a × [cとaの比]です。
書くのが面倒なものは”名付け”て省略する
上の図を見れば [cとaの比] は θが同じ直角三角形、つまり相似の三角形なら他でも成り立つと分かります。そこでこうも書けます。
c = a × [θが同じ直角三角形のcとaの比]
この[ ]を書くのが面倒なのでsinθと名付けると
c = a sinθ と書けます。サインθ。
他の辺の組み合わせも考えたら全部で6通りの式が作れます。
sin(サイン)、 cos(コサイン)、 tan(タンジェント)
secant(セカント)、cosec(コセカント)、cot(コタンジェント)です。
6つ覚えるより3つの方が楽チン
ただし、a:cはc:aの逆数で、b:cはc:bの逆数で、b:cはc:bの逆数です。
逆数の3つは省略して
sin(サイン)、 cos(コサイン)、 tan(タンジェント)をまず習います。
まとめ
直角三角形の2辺と一つの角度が分かれば、不明な辺の長さを求めることができます。例えば下の図で c = b tanθ です。θと[a, b, c, のどれか]が分かればsin, cos, tanでどの長さも分かります。
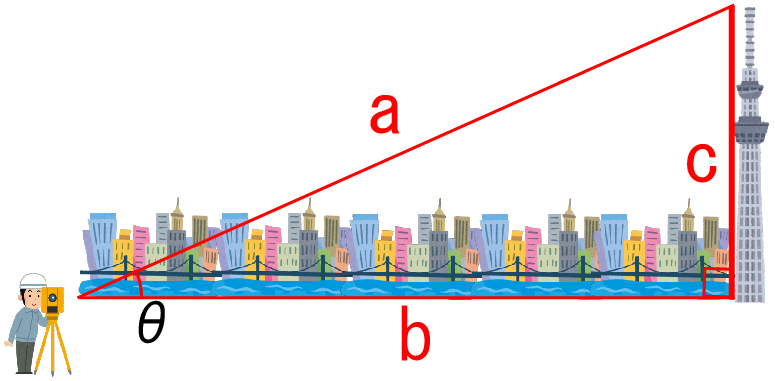
また、円運動の回転速度が分かれば t 秒後に点Pがどこにいるのかも分かります。
回転速度を角速度(ω(オメガ))と名付けたらt 秒後の角度はωtラジアンなので、 t秒後のPの位置はX座標cos ωt、Y座標sin ωtです。
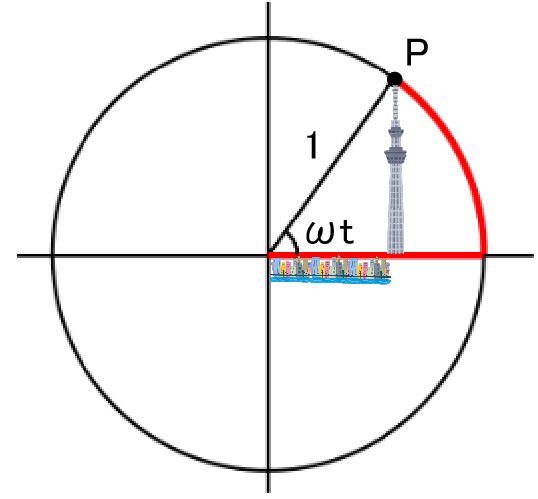
これで時間によって変化する回転運動がtを変数にした式で表すことができ、高校の物理では波を数式に表します。
最後まで読んでいただきありがとうございます。





コメント