「天才を育てた女房」とフィボナッチ数列

フィボナッチ数列とは　1, 1, 2, 3, 5, 8, 13, 21, 23, … という具合に、前の数と、その前の数を足したものが自分自身になるという数列です。
私は以前に「天才を育てた女房」というドラマを見たことでフィボナッチ数列に興味を持ちました。数学者、岡潔の物語です。

スミレは5枚、コスモスは8枚など、花びらの数は不思議なことにフィボナッチ数列に従うということがドラマでは紹介されていました。

ルネサンス期の遠近法やフラクタルによるCGのようなインパクト
葉っぱの付き方をフィボナッチ数列でプロットしてみる
フィボナッチ数列で葉の角度をシミュレーションしてみる
まとめ

ルネサンス期の遠近法やフラクタルによるCGのようなインパクト

余談になりますが、ルネサンス期のヨーロッパでは遠近法が爆発的に発展しました。
「目で見たままをこんな的確に描けるこの法則は、自然の摂理を解くことができるに違いない」
と爆発的に研究されました。
絵画・建築パース＝遠近法＝数学という構図で、この時期の絵画は現代でいう工学でもあり自然科学でもありました。

私は学生の頃（90年代）にフラクタル構造という言葉を知ったとき、ルネサンス期の研究者の気持ちが分かった気がしました。部分と全体が自己相似（再帰）になっている図形を使うことで、海岸線や植物などが自然に描けるということが、何とも言えない世界の秘密を解き明かすような気がしたものです。
そしてフィボナッチ数列を知った時にも似たインパクトを感じました。

前置きが長くなりましたが、そのような思いで自分なりの仮説を立てたり他の人の考えを知りたいと思っていた中、この書籍に出会いました。

リンク

この記事は私が考えていた事の紹介ですが、この記事をおもしろいと思ってもらえた方には上記の書籍をおすすめします。

葉っぱの付き方をフィボナッチ数列でプロットしてみる

冒頭で紹介した花びらの枚数がフィボナッチ数列に従う他にも、葉っぱの付き方やひまわりの種の並びがフィボナッチ数列に従う、オウムガイなどの渦巻きがフィボナッチ数列で描かれる螺旋に従う、という話もあります。
工業製品のように例外なしにピタリと一致するという訳にはいかないものの、実際の植物や貝などを見ていると、自然の不思議な必然性なり合理性が隠れているという気持ちになってきます。

全てについていっぺんに考えることはできないので、葉っぱに注目して考えてみました。
葉っぱにあるべき合理的とは、光合成の合理性ではないかということです。
つまり、上からあたる陽を互いに邪魔しない葉の角度が、全体最適な葉の付き方なのでは、ということです。
（本当にそうであるかどうかはさておき、自然の合理性は本当に不思議です）

フィボナッチ数列で葉の角度をシミュレーションしてみる

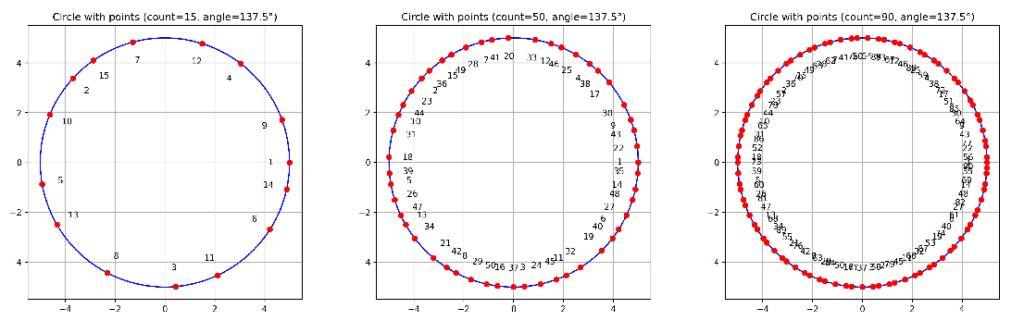
フィボナッチ数列で導かれる黄金角というものがあります。137.5度です。
これをPythonでプロットしてみます。

import numpy as np
import matplotlib.pyplot as plt

# Circle radius
r = 5

# Number of points and rotation angle (degrees)
num_points = 40       # number of points
rotation_angle = 137.5   # rotation angle (degrees)

# Coordinates for drawing the circle
theta = np.linspace(0, 2*np.pi, 300)
x_circle = r * np.cos(theta)
y_circle = r * np.sin(theta)

# Points on the circumference
angles = np.radians(np.arange(0, num_points * rotation_angle, rotation_angle))
x_points = r * np.cos(angles)
y_points = r * np.sin(angles)

# Plot
plt.figure(figsize=(6,6))
plt.plot(x_circle, y_circle, 'b')  # circle
plt.scatter(x_points, y_points, color='red', zorder=5)  # points

# Add labels always inside the circle
for i, angle in enumerate(angles, start=1):
    # ラベルを円の内側に寄せる（半径を少し小さくする）
    label_radius = r * 0.85
    lx = label_radius * np.cos(angle)
    ly = label_radius * np.sin(angle)
    plt.text(lx, ly, str(i), fontsize=10, color='black',
             ha='center', va='center')

plt.gca().set_aspect('equal', adjustable='box')
plt.title(f"Circle with points (count={num_points}, angle={rotation_angle}°)")
plt.grid(True)
plt.show()

プロットする点の数を15、50、90と増やしてみたところ。全体的な散らばりは保ちながらなかなか重ならないことがわかります。このような角度で葉っぱが付いたら光合成として合理的な構造になるのではないでしょうか。

ところで、先にできた茎や葉っぱは成長して大きくなります。つまり実際の植物の成長はらせん状になります。
そこでらせん状にして見ました。

import numpy as np
import matplotlib.pyplot as plt

def plot_sunflower_spiral(num_points=800, scale=4, point_size=3):
    """
    ヒマワリの種のようなフィボナッチ螺旋を描画（グラデーション＋小さい点）
    num_points: 種の数（点の数）
    scale: 螺旋の広がり具合（倍率）
    point_size: 各点のサイズ（小さいほど繊細）
    """
    golden_angle = np.pi * (3 - np.sqrt(5))  # 黄金角 ≈ 2.39996 rad

    # 極座標で配置
    theta = np.arange(num_points) * golden_angle
    r = scale * np.sqrt(np.arange(num_points))

    # デカルト座標に変換
    x = r * np.cos(theta)
    y = r * np.sin(theta)

    # 成長を表すグラデーション（0〜1）
    colors = np.linspace(0, 1, num_points)

    # プロット
    plt.figure(figsize=(8, 8))
    plt.scatter(x, y, c=colors, cmap='plasma', s=point_size)
    plt.title("Sunflower Spiral (Fibonacci-like, points=800)", fontsize=14)
    plt.axis('equal')
    plt.axis('off')
    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    plot_sunflower_spiral(num_points=800, point_size=3)

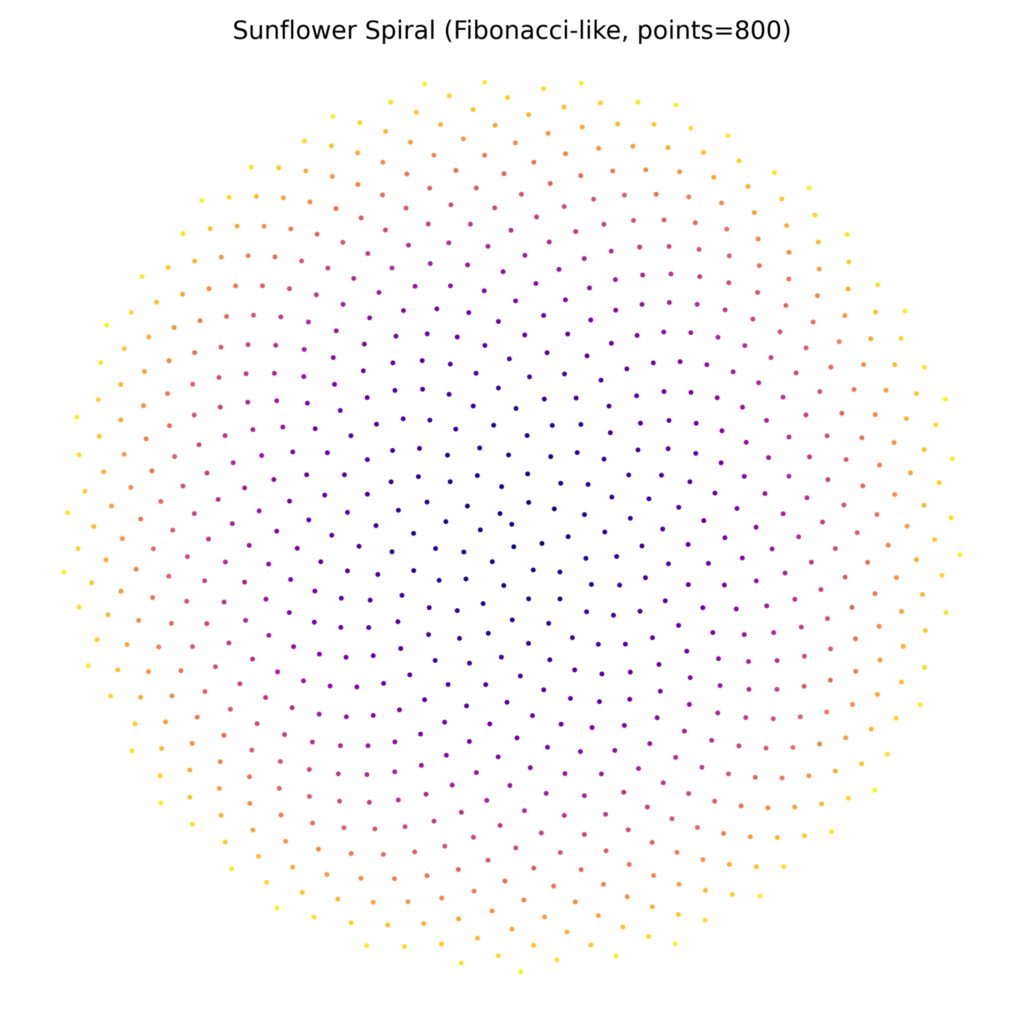
ヒマワリの種の並びと似ているように思いませんか。
松ぼっくりの笠の付き方など、色々な点で自然現象に似ていると私は思うのです。
その点がフィボナッチ数列のおもしろさだと思っています。

まとめ

遠近法、フラクタル、フィボナッチ数列はそれぞれ時代が異なるものの、自然の美しさと数学の接点を感じることができる
フィボナッチ数列は、花びらの数、葉っぱの付き方、ヒマワリの種の付き方について、自然の不思議な合理性を感じることができる
（時代による流行か）フィボナッチ数列をプロジェクトマネジメントに利用するというフレームワークもある

フィボナッチ数列と自然の不思議さについては以下の書籍が本当におすすめです。

リンク